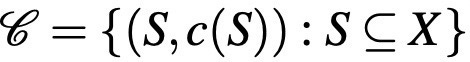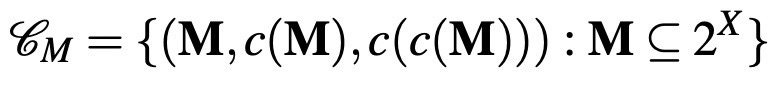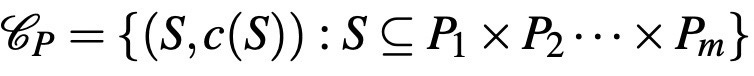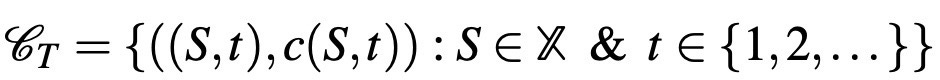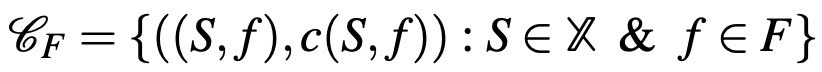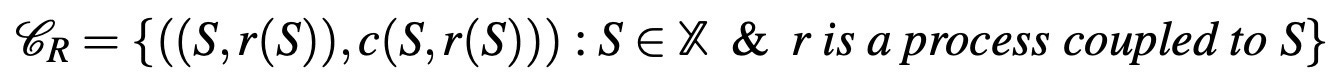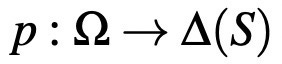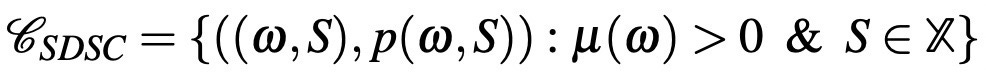Traditionally, choice theory focuses on what is observable, and therefore it is preferred to work with the set of alternatives that can also be observed by the modeler/experimenter working on the problem. Therefore, the main toolkit of a researcher includes the data on the menus such as the products you see on the shelves in a supermarket, the set of items that are listed on the online website you are shopping from, or the budget of the consumer which implies a constraint on what the consumer can afford in a shopping mall. However, to collect information regarding attention mapping of an individual, one usually needs access to more data. Here, I will discuss several types of data discussed in the literature either specifically towards identifying attention or for other purposes. Then, in the next part of the thread, I will outline the approach I am working on, which is essentially inspired by the evidence from psychology, neuroscience and especially vision studies.
Before going further, let me be more precise about what I mean by choice data: a choice data consists of the set of choice problems from which the choices of a decision-maker (DM) is observed. Think of this as an input-output model: the input DM receives is the choice data consisting of a choice problem (multiple choice problems), and her output is the choice (multiple choices or probabilistic choices). As I said, typically studies focus on what an outside observer can see as the choice data of the DM, and hence the choice data is usually assumed to be what is observable from third-person view.
The standard choice data denoted by curly C can be formalized as follows:
Here, X is the set of all alternatives, S is the choice alternatives or simply the input the DM receives, and c(S) is the choice from S. In some contexts of industrial organization, the grand set of all alternatives is usually interpreted as whatever that can be produced by a firm, and a menu of products offered by the firm is a subset of this grand set. In consumer choice, this menu is determined by the budget constraint of the consumer. So, any product available in the world is in this grand set, but which items in this grand set can be and will be produced depends on other features. An important thing to note in the sequel that this definition is quite general: it can encompass any type of data I will discuss here if suitably arranged. Therefore, an extended choice data can also be seen as a choice data in which more structure is put on the grand set of alternatives.
Thanks for reading Unreadables! Subscribe for free to receive new posts and support my work.
One of the first extensions of standard choice data is also including the choice over menus. Two leading examples are Kreps [6] and Gul and Pesendorfer [4] which model respectively the phenomena of preference for flexibility and temptation and self-control. The former phenomenon captures the observation that DMs tend to enlarge their opportunity sets in the future
(ex: smooth consumption) in order to be more flexible about what is choosable in the future, since desires and conditions can change in the future. On the other hand, the latter models a phenomenon that is working in the exactly opposite direction: the tendency of committing to smaller menus in order to prevent future cravings (such as making deal with a catering firm which offers healthy foods to a company). I call this type of data as menu-enriched choice data, which can be formalized as follows:
So, this data provides three different types of information: M is the set of menus that the DM thinks about, one can imagine this set as a collection of restaurants offering multiple food options. From this set of restaurants, the DM chooses one to buy her food, which is represented as c(M). Finally, she buys a certain food (or multiple foods) from this restaurant, represented
by c(c(M)).
Usually, the alternatives that are presented to a DM have several properties. For example, a red apple is differentiated by properties of redness, sweetness and etc., while a house can be described using its inside area, whether it has balconies or not, and whether it has access to sufficient natural lightning or not. Thus, an alternative can be viewed as a vector of properties. A natural way to extend the standard choice data is then defining the grand space of alternatives, X, in terms of the property spaces. According to this approach, each alternative can be described using its values in each property. So, X is equal to a space which can be denoted as P_{1} × P_{2} · · · × P_{m} assuming that there are m properties in the world where m is a natural number. Consider a specific property k and its space P_{k}. If this property is a binary one, then P_{k} = {0, 1}. The most natural example that comes to mind is still the most natural example that comes to mind, even for queer theorists. Another example is the color of a fruit: we usually perceive as a red apple as if only red and do not carry another color (at least in a dominant way). On the other hand, color is known to be expressed as a combination of three dimensions that does not take binary values, see Gardenfors [3]. To sum, the set of all choice problems in this case can be written as:
I refer to this type of data as property-based choice data.
Another type of data frequently used is repeated choice data, which is a straightforward extension of the standard choice data: the choices of a DM or multiple DMs collected over time. Using a discrete time framework and denoting a generic time period with t, the DMs choices are observed from (S,t) if she is presented a menu of alternatives S at period t. So, the set of all choice problems in repeated choice data can be written as:
Even though the main toolkit excluded parts of the environment that we deem less observable for a long time, the results of experiments and other empirical work showed the importance of other factors in the environment. The seminal work of Kahneman and Tversky[5] showed the importance of frames. A frame is usually interpreted as a payoff-irrelevant factor that would not normally change the incentives of a decision problem, but possibly effective in the perception of it. Thus, one would expect a fully rational individual would not be affected by perceptional limitations, and chooses the best option according to her preferences irrespective of the frames. The observation that this is not the case is a powerful demonstration of the boundedness of cognition in humans. Hence, models in the literature started to incorporate the frame of a choice problem as on explicit part in the formulation of theories of decision-making. The work of Rubinstein and Salant [10] and Masatlioglu and Ok [7] are two models that explicitly
corporate frames. This presents an extended choice data of the standard choice data which only includes the choice alternatives that the individual can choose from. Let F denote the (finite) set of frames. The frame-dependent choice data is defined as:
Note that repeated choice data is a special case of frame-dependent data, which provides a simple and natural example of frames. Certainly, time cannot be treated in general as a payoff irrelevant factor, since it simply affects the discount rate of the consumer or all of the environmental conditions depend directly on time. However, it can be treated just as the clock-time of when the choice is made, and this will make it payoff-irrelevant at the abstract level.
Another type of data which carries very important information about the decision-making process is what I call process-choice data. Process choice data collects information about the process of the DM that culminates in the final choice. Before recent advances in the technology, such data is typically collected using verbal reports, for a pioneering work discussing
this see Ericsson and Simon [2]. For instance, one can simply ask a DM about how she thinks about the choice problem presented. Another frequently collected statistic relevant to the choice process is response-time, which measures the time length between the presentation of a choice problem and the final choice. Although there is almost a conventional distrust to verbal reports because of its subjective nature (and possibly because the ultimate superiority of the scientist compared to the subject in the eyes of the experimenter), response time is accepted as a conventional tool that is useful (see for instance Rubinstein [9]). Experimental studies and developing techniques in neuroscience such as fMRI enabled further advances in the type of data that can be collected. Now scientists are able to observe the changes in the chemico-electrical structure of the brain that happens during choice process. This opens a huge and unending process of measuring neural correlates of any concept relevant to decision-making. All of these can be modeled using a pair of (S, r) where r denotes the additional data collected about choice process when the DM is presented alternatives in S. For example, a neuroscientist can present a choice problem involving two alternatives, and measure the changes in the blood-oxygen level in the brain using fMRI and BOLD-contrast imaging. This is an improvement over the standard choice data: now the scientist has access to both the alternatives presented (S) and what happens in the brain when these are presented and before a final choice is made. In this sense, process-choice data can be viewed as a "real extension" that is not made simply explicit from the grand set X (but still can be captured by a suitable redefinition of the standard choice data). Thus:
An important special case is belief data. Nyarko and Schotter [8] presents a nice example of this in which they elicit beliefs by directly asking the participants (an example of verbal report). Thus, they collect the beliefs of the individuals as the choice process of the individual.
Anoher line of work which considers another type of extended choice data is the rational inattention theory which uses tools of information theory. Both theoretical and experimental work on rational inattention continue to grow. The type of extended choice data used in this framework is called state-dependent choice data (see Caplin[1]). What is state-dependent choice data? To better explain this, I will provide a short introduction to the model of rational inattention, taken from Caplin [1]. Let Ω be the set of finite states of the world with a generic element ω. The DM can choose from a finite set of actions, which can be modeled by assuming X is the set of actions. Assume that the preferences of the DM can be represented by a state-dependent utility function u :X × Ω → R where u(x, ω) is the utility DM gets in state ω when she implements action x. All individuals have a prior μ over the set of all worlds, an initial belief (from the viewpoint of the modeler). This defines a decision problem in the rational inattention framework, a pair (μ, S) for μ ∈ ∆(Ω) and S in X. Given a decision problem (μ, S), the DM’s choice is described by the stochastic choice function p such that:
The observer in this framework is assumed to have access to the possibly probabilistic choices of the DM conditional on the state of the world. Hence, the rational inattention framework is a choice-theoretic framework: it relies on the choice data of the DMs. Observe that this data has even stronger requirements than what is required in traditional choice-theory models: the modeler/experimenter can observe the states of the world. Note that even though the DM chooses her action based on a prior belief, in reality only one state of the world realizes, say ω. Still, the experimenter needs to measure the prior belief of the DM observes this state and the choices of the DM at this state, as it will be apparent in the following definition. Now I am ready to define the type of data used by this theory, called state-dependent stochastic choice data (SDSC) by Caplin [1]:
So, this data enables access to the set of available actions S with the prior beliefs of the DM over the states of the world. In addition to this, the experimenter can observe possibly probabilistic choices of the DM conditional on the state of the world.
This completes a brief introduction to several types of extended choice data which can be used to identify attention (although not intended so in the beginning). The next part of the thread will talk about awareness-based choice data, a type of data I think useful in getting more detailed information on the attention process of the DM, which is influenced by the separation between top-down and bottom-up attention.
References:
[1] Caplin, A. (2016). Measuring and modeling attention. Annual Review of Economics, 8, 379-403.
[2] Ericsson, K. A., and Simon, H. A. (1980). Verbal reports as data. Psychological review, 87(3), 215.
[3] Gardenfors, P. (2014). The geometry of meaning: Semantics based on conceptual spaces. MIT
press.
[4] Gul, F., and Pesendorfer, W. (2001). Temptation and self control. Econometrica, 69(6), 1403-1435.
[5]Kahneman, D. and Tversky, A. (1974). Judgment under Uncertainty: Heuristics and Biases: Biases in judgments reveal some heuristics of thinking under uncertainty. science, 185(4157), 1124-1131.
[6] Kreps, D. M. (1979). A representation theorem for" preference for flexibility". Econometrica: 565-577.
[7] Masatlioglu, Y., and Ok, E. A. (2005). Rational choice with status quo bias. Journal of economic theory, 121(1), 1-29.
[8] Nyarko, Y., and Schotter, A. (2002). An experimental study of belief learning using elicited beliefs. Econometrica, 70(3), 971-1005.
[9] Reutskaja, E., Nagel, R., Camerer, C. F., and Rangel, A. (2011). Search dynamics in consumer choice under time pressure: An eye-tracking study. American Economic Review, 101(2), 900-926.
[10] Rubinstein, A. (2007). Instinctive and cognitive reasoning: A study of response times. The Economic Journal, 117(523), 1243-1259.
[11] Rubinstein, A. and Salant, Y. (2008). (A, f): choice with frames. The Review of Economic Studies, 75(4), 1287-1296.
1
This separates the philosophy of choice theory from philosophy of decision theory in the primitive level: choice theory is specifically grounded on observables such as choice data (hence the name choice theory), while decision theory takes a more mentalist attitude by including objects such as preferences and beliefs potentially
observable. For a discussion related to this, see Moscati[?]. Another important point is made by Caplin[?] who notes that choice theory approach is a transition led by Samuelson[?] which represents a deviation from the psychophysical approach of “marginal utilists” such as Bentham to a “behaviorist” tradition not well-accepted in philosophers, see Thoma[?].
2
See for instance Reutskaja et al.[9].